Streifentafel
Die Streifentafel wird in der modernen Mathematikdidaktik zur Bruchrechnung anderen Veranschaulichungsmitteln vorgezogen. Warum das so ist und warum der Linearbruchkasten von Plackner so gut in dieses Konzept passt, erläutert der Artikel.

Grundvorstellungen
Die Entwicklung tragfähiger mathematischer Konzepte basieren auf dem Aufbau von Grundvorstellungen. Viele Einführungen stellen den Bruch als Anteil eines Ganzen dar. Das können Anteile von Torten oder Pizzen sein, Stücke von Schokotafeln, Papierfaltungen, gängige Angaben zu Gewichten oder Flüssigkeiten in Rezepten, Geldmengen etc.
Darstellungsformen
Hier kann man nach dem „EIS-Prinzip“ wieder mehrere Ebenen unterscheiden. Beim handlungsorientierten (enaktiven) Vorgehen zerschneide ich z.B. einen Apfel in mehrere gleich große Teile, breche Schokostücke von einer Tafel ab etc.
Die meisten beschriebenen Darstellungsformen sind allerdings ikonischer Art (zweidimensional). Doch auch diese unterscheiden sich weiter. Kann ich mit der Kreisdarstellung gleich große Anteile zeigen, lässt die Streifentafel weitere Möglichkeiten zu, weshalb sie in Bruchrechenkonzepten bevorzugt zum Einsatz kommt.
Die Vielseitigkeit der Streifentafel
Dieses Anschauungsmittel wurde von Prediger eingeführt und hebt die Möglichkeit hervor, Brüche direkt zu vergleichen. Ihr Konzept liegt dem Buch „Mathe sicher können-Brüche“ (Cornelsen) sowie dem darauf basierenden Diagnose- und Förderkonzept von Mathe sicher können zugrunde, welches neben der Streifentafel auch weiteres Anschauungsmaterial und Arbeitsblätter kostenlos zur Verfügung stellt.
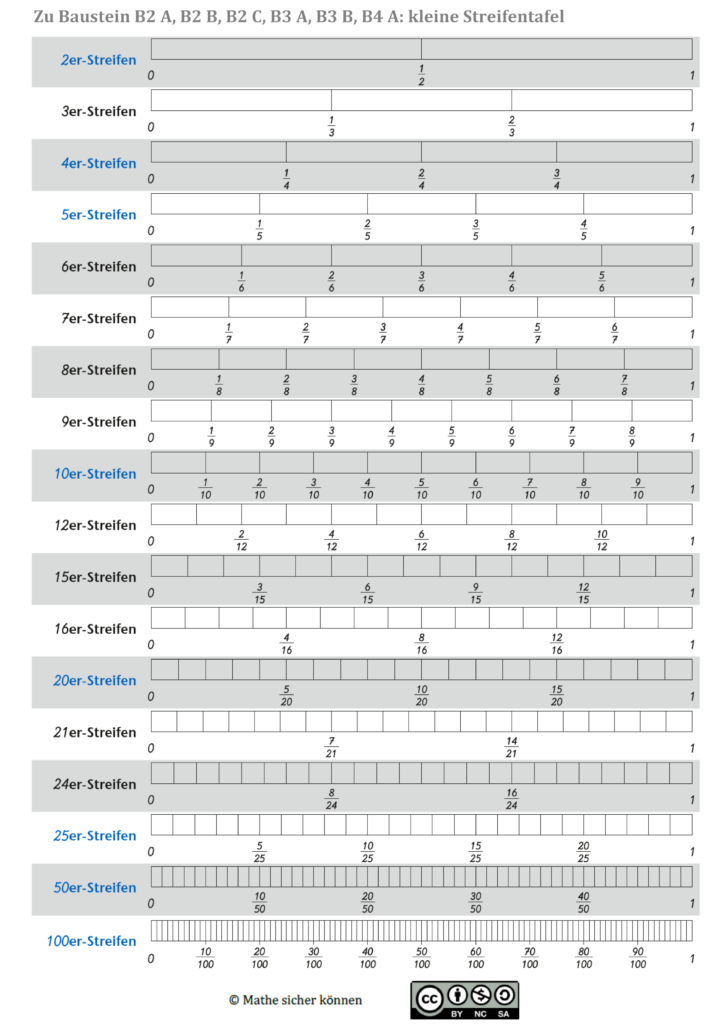
Die einzelnen Möglichkeiten zum Einsatz der Streifentafel
- Anteile vergleichen mit Bruchstreifen
- Suche z.B. Brüche wie 1/2, 1/3, 1/4, 1/6.
- Wie sieht man, ob z.B. 3/4 genauso groß ist wie 9/12?
- Finde möglichst viele Anteile in der Streifentafel, die genauso groß sind wie z.B. 2/6?
- Vergröbern und Verfeinern: Vergröbere z.B. 6/8 in Viererstreifen oder verfeinere den Bruch in Sechzehnerstreifen.
(In Analogie zum Vergröbern und Verfeinern sprechen wir später vom Erweitern und Kürzen) - Brüche durch Vergleich auf der Streifentafel in Hundertstelbrüche umwandeln (1/2 gleich 50/100 gleich 50%)
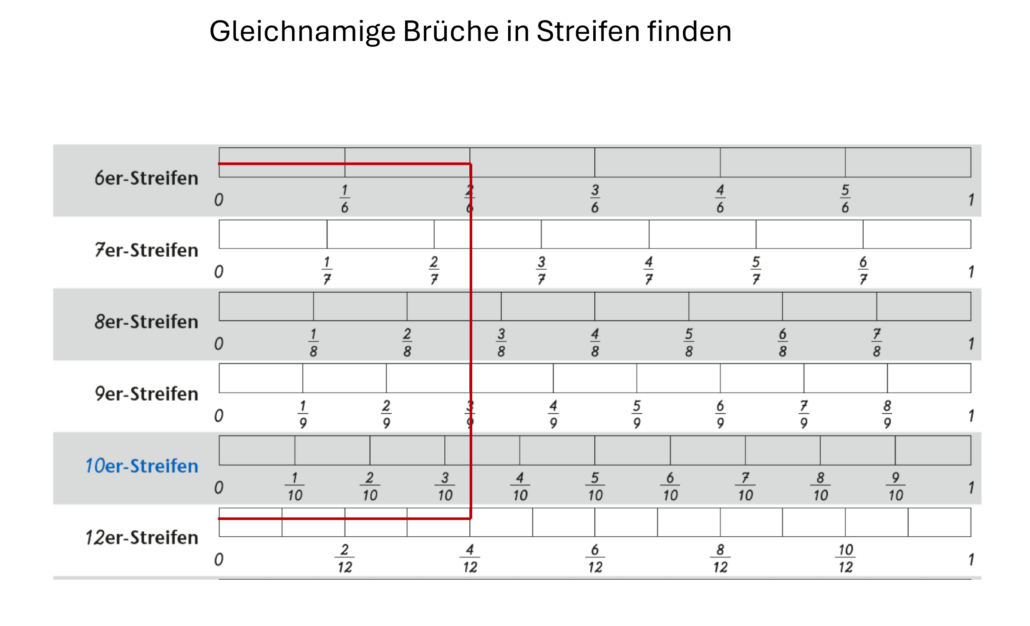
- Gleichnamige Brüche auf der Streifentafel finden, z.B. 2/6 gleich 4/12.
- Anteile mit verschiedenen Nennern zusammenfügen oder wegnehmen, z.B. 1/2 + 1/3.
An dieser Stelle kommt aber auch die Streifentafel an ihre Grenzen, ich muss auf dem Arbeitsblatt den Sechserstreifen 3-mal kopieren, um das Ergebnis übersichtlich darstellen zu können.
Hier findest du alle Übungsformen im PDF-Format.
Der Linearbruchkasten von Plackner
Der Linearbruchkasten von Plackner bedient die gleichen Arbeitsprinzipien wie die Streifentafel, setzt aber auf der enaktiven, handlungsorientierten Ebene an. Ich kann alle Bruchteile von 1/2 bis 1/20 herausnehmen, direkt nebeneinanderlegen und vergleichen. Das Vergröbern und Verfeinern (Erweitern und Kürzen) kann ich in gesonderten Leisten darstellen, ich kann gleichnamige Brüche finden und dann direkt addieren. Die Umwandlung in Hundertstelbrüche ist nicht möglich, so feine Unterteilungen sind in Holz nicht zu erstellen, aber es gibt Leisten zum Ablesen der Prozente, ebenso solche zum Ablesen von Dezimalzahlen.


Ich arbeite in Kombination mit beiden Materialien, zuerst handlungsorientiert, dann ikonisch oder auch symbolisch mit Arbeitsblättern. Die Schüler lieben den präzise gearbeiteten Kasten mit Geruch des würzigen Öles, der auch noch nach über einem Jahr vom Holz ausströmt. Ein wertiges, langlebiges, wenn auch nicht billiges Arbeitsmittel, welches die neuesten Wege der Mathematikdidaktik mitgeht.
Siehe auch andere Blogartikel zu Mathematikinhalten der Sekundarstufe I wie lineare Funktionen, Prozentrechnung, Satz des Pythagoras und Gleichungen mit einer Unbekannten.