Der Satz des Pythagoras steht für den Bereich geometrische Flächenberechnungen. Er lässt sich mit den Montessori-Rahmen leicht, verständlich und handlungsorientiert darstellen und begreifen.

Inhaltsbereiche für den Hauptschulabschluss NRW
- Grundlagen des Rechnens
- Rechnen mit Größen
- Gleichungen
- Funktionaler Zusammenhang
- Prozentrechnung und Zinsrechnen
- Stochastik
- Der Satz des Pythagoras (Geometrie der Ebene)
- Körper
Definition: In einem rechtwinkligen Dreieck ist die Summe der Flächeninhalte der beiden Quadrate über den Katheten gleich dem Flächeninhalt des Quadrats über der Hypotenuse. Der Satz gilt für alle rechtwinkligen Dreiecke.
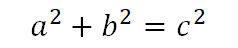
Der erste Montessori-Rahmen


Es werden 2 Darstellungen des Pythagoras mit weißen, gleichschenkligen und rechtwinkligen Dreiecken gezeigt. Bei der zweiten Figur der ersten Darstellung sind das gelbe und blaue Quadrat über den Katheten in je 2 Dreiecke unterteilt, das rote Quadrat unter der Hypotenuse in 4 Dreiecke. Nun setzt man je zwei rote Dreiecke über die Katheten und die 2 blauen und gelben Dreiecke unter die Hypotenuse: Es ist ersichtlich, dass die beiden kleineren Kathetenquadrate zusammen flächengleich sind mit dem Hypotenusenquadrat.
Der Satz des Pythagoras, zweiter Rahmen
Ausgehend von einem ungleichseitigen, rechtwinkligen Dreieck werden die Quadrate über den Katheten und der Hypotenuse durch kleine, zentimetergroße metallene Plättchen dargestellt. Wieder ergeben die Plättchen über den Katheten zusammen die Fläche des Quadrats über der Hypotenuse und deren Plättchen füllen die Fläche der beiden Kathetenquadrate, sind also flächengleich.



Der Satz des Pythagoras, dritter Rahmen
Die Quadrate über den Katheten und der Hypotenuse werden durch flächengleiche Parallelogramme ersetzt. Durch Verschieben und Vergleichen aller Teile wird die Flächengleichheit des gelben Parallelogramms, des gelben Quadrats und des großen roten Rechtecks bewiesen. Gleiches gilt für das kleinere blaue Parallelogramm, das blaue Quadrat und das schmalere rote Rechteck.

Eine ausführlichere Darstellung findet bei Achim Cuypers: Geometrie in Kinderhaus und Montessori-Grundschule (Herder Verlag). Leider ist es überwiegend nur noch als E-Book verfügbar. Hier noch ein Link zu einer gedruckten Auflage.
Siehe auch meine weiteren Beiträge zur Prozentrechnung, zu linearen Funktionen und zu Montessori-Material in der Mathematik allgemein.